บทความชุด: Functional Programming
รวมเนื้อหาเกี่ยวกับการเขียนโปรแกรมแนว Functional และหัวข้ออื่นๆ ที่เกี่ยวข้อง
- ตอนที่ 1 Pure, First-Class, High-Order, พื้นฐานแห่ง Functional Programming
- ตอนที่ 2 Lambda Function and Closure ฟังก์ชันทันใจและพื้นที่ปิดล้อม!
- ตอนที่ 3 map filter reduce และเพื่อนๆ พระเอกแห่งโลก Functional
- ตอนที่ 4 โครสร้างแบบ Pair และ Either กับ List Comprehension การสร้างลิสต์ฉบับฟังก์ชันนอล
- ตอนที่ 5 Lazy Evaluation ขี้เกียจไว้ก่อนแล้วดีเอง?!
- ตอนที่ 6 Recursive Function ฟังก์ชันเวียนเกิด, เขียนลูปไม่ได้ทำยังไง? มาเขียนฟังก์ชันเรียกตัวเองแทนกันเถอะ!
- ตอนที่ 7 Curry, Partial Function
- ตอนที่ 8 Functor, Monad
- [บทความปี 2015] มารู้จักกับ Functional Programming สิ่งที่คุณต้องรู้ในตอนนี้กันเถอะ
- Function ทำงานยังไง?, ในมุมมองของโปรแกรมเมอร์สาย Imperative
Category Theory & Lambda Calculus
Lambda Calculus พื้นฐานสู่ Functional Programming
บทความนี้เกิดขึ้นตอนที่กำลังเขียนซีรีส์ Functional Programming อยู่ แล้วมีส่วนพูดถึงแนวคิดทางวิชาคณิตศาสตร์ที่เรียกว่า Lambda Calculus ซึ่งเขียนไปเขียนมาก็ดูเหมือนมันจะยาวเกินไปจนขอแยกออกมาเป็นอีกบทความหนึ่งเลยน่าจะดีกว่า
กำเนิด Lambda Calculus (ที่ไม่ใช่แคลคูลัส)
เชื่อว่าในครั้งแรกที่เราได้ยินชื่อคำว่า "แลมด้า แคลคูลัส" สิ่งแรกที่เราคิดน่าจะเป็นวิชาคณิตศาสตร์ที่เรียกว่า แคลคูลัส ที่เราเรียนกันในวิชาฟิสิกส์หรือพวกวิชา Differential Equation ... เอาเป็นว่ามันคือคนละวิชากันละกัน เคยรู้อะไรเกี่ยวกับแคลคูลัสมา ลืมๆ มันไปก่อน
แล้วสำหรับ Lambda Calculus นี้เกิดขึ้นมาตั้งแต่เมื่อไหร่ แล้วเกิดขึ้นมาเพื่ออะไร เราต้องย้อนกลับไปในช่วงที่เครื่องจักรสำหรับการคำนวณที่เรียกว่าคอมพิวเตอร์ถูกสร้างขึ้นมาในช่วงยุคปี 1945 โน้น~
คอมพิวเตอร์ถูกสร้างขึ้นโดยนักวิทยาศาสตร์และนักคณิตศาสตร์ (โดยน่าจะเป็นนักคณิตศาสตร์เป็นหลัก) ซึ่งนักคณิตศาสตร์พวกนั้นก็กำลังสงสัยกันว่า "การคำนวณ" นั้นที่แท้จริงมันคืออะไร ทำไมมันถึงคำนวณได้ อะไรบ้างที่เอามาคำนวณได้ หรืออะไรบ้างที่คำนวณไม่ได้ ... ฟังดูอาจจะแปลกๆ ซะหน่อย มาสงสัยอะไรกันที่มัน abstract แบบนี้ การคำนวณก็คือการคิดเลขอะไรบางอย่างไม่ใช่เหรอ?
แต่ต้องลองนึกดูนะครับ ว่าในขณะนั้น มนุษย์ต้องการสร้างเครื่องจักรที่สามารถคิดเลขได้ ไม่ใช่ระดับง่ายๆ แบบเครื่องคิดเลขที่ต้องให้มนุษย์มานั่งกดเลขๆ แต่เป็นเครื่องจักรระดับที่สามารถคำนวณโจทย์เลขหรืออะไรบางอย่างที่มีความซับซ้อน หรือมีขั้นตอน มีลำดับอะไรพวกนั้นได้
ดังนั้นเราเลยต้องเข้าใจให้ได้ซะก่อน ว่าหัวใจสำคัญของการคำนวณมันคืออะไรกันแน่? เราจะได้เอาแนวคิดนั้นมาสร้างเครื่องคอมพิวเตอร์ได้
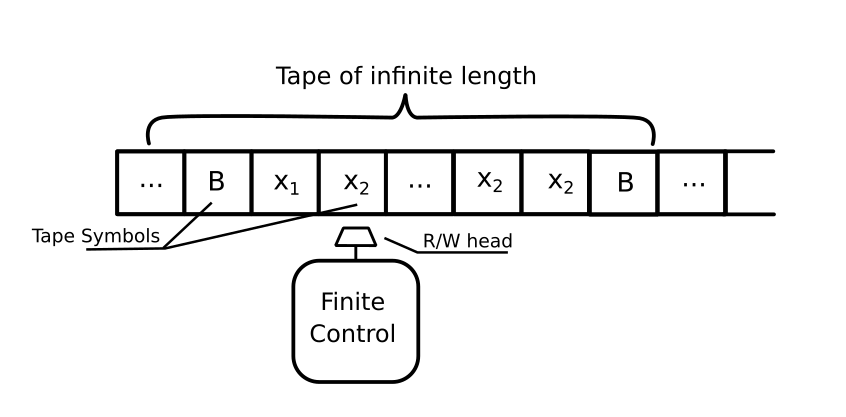
สุดท้ายแล้วก็มีตัวเลือกหนึ่งที่ ซึ่งเป็นแนวคิดที่ต่อมานำมาใช้สร้างคอมพิวเตอร์นั่นก็คือ Turing Machine หรือเครื่องจักรของทัวริง ที่ออกแบบและสร้างโดย Alan Turing นั่นเอง
ต้องอธิบายเพิ่มนิดนึงว่าถึงแม้เราจะเรียกว่า Turing Machine แต่จ้าเครื่องจักรตัวนี้ไม่มีจริงนะครับ เป็นแค่เครื่องจักรเสมือน เป็นหลักการคิดในอุดมคติเท่านั้น เวลาใช้ก็เขียนๆ ทดๆ กันลงในกระดาษนี่แหละ
แต่ก็ดูเหมือนมีคนเอาเครื่องจักรในความคิดนี้มาสร้างเป็นเครื่องจริงๆ อยู่เหมือนกัน ลองเสิร์จใน Google ดูได้
หลัการคำนวณของทัวริงนั้นจะใช้แนวคิด Stored-Procedure คือมีเมมโมรี่เป็นหน่วยความจำเอาไว้เก็บตัวแปร แล้วก็มีส่วนประมวลผลที่จะทำคำสั่งแล้วเปลี่ยนแปลงค่าตัวแปรนั้นไปเรื่อยๆ จนกว่าจะได้คำตอบออกมา
คุ้นไหมครับ?
ถ้าคุณเรียนสายคอมพิวเตอร์มา คุณน่าจะคุ้นแนวคิดนี้ไม่มากก็น้อย (ละมั้ง?) เพราะมันคือแนวคิดที่ต่อมา John Von Neumann นำมาสร้างเป็นเครื่องจักรสำหรับคำนวณที่ต่อมากลายเป็นต้นแบบของคอมพิวเตอร์ที่ใช้งานได้จริงๆ เครื่องแรกของโลก แล้วก็เป็นโมเดลที่เราใช้กับคอมพิวเตอร์มาจนถึงปัจจุบันด้วย
ใช่แล้ว! มันคือหลักการของ CPU และ Memory (หรือ RAM) นั่นเอง
ใครสนใจเรื่อง Turing Machine ลองหาข้อมูลเพิ่มเติมอ่านดูได้นะ แต่ในบทความนี้จะพูดแค่นี้ก่อน ถ้ามีโอกาสจะกลับมาเขียนเกี่ยวกับมันเพิ่มอีกที
แต่นอกเหนือจาก Turing Machine แล้วก็ยังมีแนคิดหนึ่งซึ่งพัฒนาโดยนักคณิตศาสตร์ชาวอเมริกันชื่อว่า Alonzo Church (เข้าคนนี้เป็นอาจารย์ที่ปรึกษาระดับปริญญาเอกของ Alan Turing ครับ) นั่นก็คือ Lambda Calculus นั่นเอง! (กว่าจะเข้าเรื่อง ฮา)
เนื่องจากแนวคิดนี้มันเป็นหลักการของการคำนวณ มันเลยถูกตั้งชื่อว่า "Calculus" รายละเอียดลึกๆ เหมือนจะพิสูจน์ย้อนกลับไปถึงพื้นฐานของวิชาเลขที่เราเรียนๆ กันตอนประถมได้เลย แต่เราจะมาโฟกัสกันเฉพาะในส่วนของ Computer-Science กันเท่านั้นพอ
มีคำที่อธิบายความสำคัญของ Lambda Calculus ได้อย่างดีนั่นคือ
Everything that can be Computed, can be computed by Lambda Calculus.
อะไรก็ตามที่สามารถคำนวณได้, มันจะถูกคำนวณได้ด้วยแลมด้าแคลคูลัส ... เท่จริงๆ
(แปลว่าถ้าแลมด้าแคลคูลัสประมวลผลไม่ได้ คอมพิวเตอร์ก็ประมวลผลข้อมูลแบบนั้นไม่ได้เช่นกัน)
ความจริงแล้ว หลักการนี้ใช้กับ Turing Machine ได้ด้วย ข้อแตกต่างคือ ในขณะที่ทัวริงใช้หลักการของ State-Base Computation, อาจารย์ของเขากลับแก้ปัญหาเดียวกันด้วยหลักการของ Functional Notation Computation แทน -- เมื่อเป็นแบบนี้ เราเลยสรุปได้อีกข้อหนึ่งคือ Turing Machine และ Lambda Calculus นั้นสามารถแปลงไปเป็นอีกตัวนึงได้ในทุกกรณี
Symbol Processor
เวลาเราเขียนโปรแกรม สิ่งที่เราทำคือเขียนโค้ดลงไป ซึ่งโค้ดพวกนั้นก็อยู่ในรูปของตัวอักษาบ้าง ตัวเลขบ้าง แล้วก็นำโค้ดนั้นไปแปลงคอมไพล์เป็น Machine Code อีกทีนึง แต่ถ้ามองพวกนี้รวมๆ แล้วมันก็คือชุดคำสั่งที่เอามาเรียงต่อกัน จะมองเป็น "สัญลักษณ์" หรือ Symbol ก็ได้
ดังนั้นเราเลยสามารถสรุปได้อีกแบบหนึ่งว่าคอมพิวเตอร์นั้นก็คือตัวประมวลผลสัญลักษณ์ หรือ Symbol Processor นั่นเอง
แต่สิ่งที่น่าสนใจคือ ... การเอาสัญลักษณ์พวกนี้มาเรียงกันแล้วมันประมวลผล/คำนวณ/หรือทำงานเพื่อให้ได้คำตอบมาได้อย่างไร?
Lambda Calculus Syntax: หลักไวยากรณ์
คอนเซ็ปไวยากรณ์หลักๆ มีอยู่ 3 ตัวด้วยกัน คือ
- Abstraction -
λx.M - Application -
(M1 M2) - Value -
V
โดยที่ตัว M แทนมาจาก "Lambda Term" หรือก็คือพวก Expression-สมการ นั่นเอง
ส่วนสัญลักษณ์ λ คือตัวแลมด้าเล็ก เป็นอักษรกรีก ซึ่งถ้าเป็นแลมด้าตัวใหญ่จะใช้สัญลักษณ์ Λ
มีแกรมม่าอยู่แค่ 3 ตัวนี้ ตามทฤษฎีบอกว่าสามารถเขียนได้ทุกโปรแกรมในโลกนี้แล้ว!
มาดูตัวแรกกันก่อน
Abstract: λx.M
เทียบได้กับการประกาศฟังก์ชันขึ้นมา (Function Declaration) ส่วนฟังก์ชันนั้นให้มองว่ามันเป็น Black-Box หรือกล่องดำ ที่สามารถรับ Input เข้าไปได้ แล้วให้ Output ออกมา เขียนแทนด้วยสัญลักษณ์แบบนี้
f(x) = x * 10
อันนี้หมายความว่า เราสร้างฟังก์ชัน ชื่อ f ขึ้นมา ซึ่งรับ Input x เข้าไป แล้วเอาไปคำนวณด้วยการ * 10
ถ้าเราจะเอาฟังก์ชันมาใช้งาน เราก็เรียกใช้ได้แบบนี้
f(5) //ซึ่งจะได้ผลออกมาคือ 5 * 10 เท่ากับ --> 50
ลองมาดูตัวอย่างในชีวิตจริงกันบ้าง เช่น
มีฟังก์ชันสำหรับคำนวณค่าจอดรถ
อาจจะรับ Input เป็นตำนวนชั่วโมงที่จอดรถไป
แล้วคืน Output ออกมาเป็นราคาที่ต้องจ่าย** ส่วนจะคำนวณค่ายังไง ถือว่าไม่ต้องสนใจ (ในมุมมองคนที่เรียกใช้งาน ไม่ต้องสนใจ / แต่คนที่สร้างฟังก์ชันก็ต้องสนอยู่ดีนะ)
โดนจากตัวอย่างข้างบน สมมุติว่าเราตั้งกฎว่าค่าจอดรถชั่วโมงละ 10 บาท ถ้าเราเอาไปเขียนในรูปของฟังก์ชัน เราจะเขียนได้ว่า
parking_fee(hour) = hour * 10
ใน Lambda Calculus, หลักการสร้างฟังก์ชันก็เหมือนเดิมแบบนี้นี่แหละ แต่เปลี่ยนสัญลักษณ์แทน เป็นแบบนี้
λx . x * 10
คือเปิดด้วยสัญลักษณ์ λ ตามด้วยตัว Input (หรือเรียกว่า Parameter) เข้ามาจำนวนหนึ่ง (ในตัวอย่างตั้งชื่อว่า x) ตามด้วยตัว . ซึ่งเป็นการบอกว่าตอนไปจะเป็นส่วน body ของฟังก์ชันของเรา
เพิ่มเติมนิดนึง คือตามนิยามของฟังก์ชันที่เราเคยเรียน มันกำหนดว่า Input สามารถมีได้หลายตัว (แต่ Output จะต้องมีแค่ 1 ตัวเท่านั้น) เราสามารถประกาศฟังก์ชันได้แบบนี้
// รับ x และ y เข้ามา แล้วคำนวณหาผลบวกของ x กับ y
λx . λy . x + y
// รับค่า u, t, a เข้ามาแล้วคำนวณหาค่า S (อันนี้เป็นสูตรการเคลื่อนที่แนวเส้นตรง ข้ามๆ ไปก็ได้)
λu . λt . λa . ut + (1/2)at^2
ข้อสังเกต: การสร้างฟังก์ชันใน Lambda Calculus นั้นจะไม่มีการแบ่งส่วน parameter/body อย่างชัดเจน คือใช้ . เป็นตัวเชื่อม ส่วนอันไหนเป็นส่วนของ input parameter ก็จะมีสัญลักษณ์ λ นำหน้า เพราะจริงๆ แล้วนิยามของฟังก์ชันในเรื่องนี้ต่างกับฟังก์ชันที่เรารู้จักกัน นั่นคือฟังก์ชันมี input ได้แค่ parameter เดียว! ดังนั้นถ้าเราต้องการส่ง parameter มากกว่า 1 ตัว เราจะมีเทคนิคหนึ่งที่เอามาใช้ นั่นคือ "Currying" ซึ่งไว้เราจะพูดกันต่อในบทความชุด Functional Programming
Application: (M1 M2)
หลังจากสร้างฟังก์ชันขึ้นมาแล้ว เราก็ต้องมีการเรียกใช้งานฟังก์ชัน (Call Function) ซึ่งเราเรียกว่า Application หรืออาจจะแปลว่ามันคือการ "Apply expression M1 ด้วย expression M2" ก็ได้
สมมุติเราจะลองเอาชั่วโมงที่เราจอดรถไป 5 ชั่วโมงเมื่อกี้มาใช้กับฟังก์ชันที่เราประกาศไปเมื่อกี้ ก็จะเขียนได้ว่า
(λx.x*10 5)
หากมองเป็นภาษาโปรแกรมที่เราคุ้นชินกัน มันก็คือการสร้าง "Anonymous Function" (หรือที่บางภาษาก็เรียกตรงๆ เลยว่า "Lambda") ขึ้นมาหนึ่งตัว แล้วสั่งให้มันทำงานเลยโดยส่ง input เข้าไปด้วย แบบนี้
//declare function f
function f(x){
return x * 10;
}
//call f
f(5);
//หรือสร้างฟังก์ชันแล้วสั่งให้มันทำงานทันทีเลย แบบนี้
(function(x){
return x * 10;
})(5);
ดังนั้นการเรียกใช้
(λx.x*10 5)
ก็จะมีความหมายว่าเอา 5 เข้าไปแทนที่ x ซะ จะได้ว่ามันก็คือ
(5*10)
หรือสมมุติว่าเราส่งค่าอื่นเข้าไป เช่น
(λx.x*10 a^b+100)
// ก็จะได้เป็น
( (a^b+100) * 10)
เอาล่ะ จบกันไปแล้ว, เดี๋ยว!? อะไรนะ แค่นี้เหรอ ... ใช่แล้ว คอนเซ็ปคร่าวๆ ของ Lambda Calculus มีแค่นี้แหละ แต่ถ้าให้แค่นี้หลายๆ คนน่าจะงงกันเลยว่าไม่เห็นมีอะไรเลย ตกลงมันดีจริงเหรอ หรือเอาไปใช้งานยังไง ต่อไปเราจะมาดูตัวอย่างกันใช้งานกันนะ
Ex1: TRUE, FALSE และ NOT
ตัวอย่างแรกจะเป็นการสร้าง TRUE และ FALSE ขึ้นมา จากสร้างเราจะสร้างฟังก์ชันสำหรับทำ operation NOT กัน
เริ่มด้วยการ declare ว่าอะไรคือ TRUE, FALSE โดยขอกำหนดว่า
TRUE = λx . λy . x
FALSE = λx . λy . y
หรือจะมองง่ายๆ แบบนี้ก็ได้ (เปลี่ยนชื่อตัวแปรซะหน่อย)
TRUE = λfirst . λsecond . first
FALSE = λfirst . λsecond . second
อธิบาย: ฟังก์ชัน TRUE คือการที่เรารับค่าเข้าไป 2 ค่า --> แล้วตอบค่าตัวแรกกลับไป
ส่วนฟังก์ชัน FALSE คือการที่เรารับค่าเข้าไป 2 ค่า เหมือนกันเลย --> แต่จะตอบค่าตัวที่สองกลับไป
อ่านมาถึงตรงนี้อาจจะงงว่า การกำหนด TRUE, FALSE แบบนี้ทำไปทำไมกัน? ทนอ่านต่ออีกนิดนึงนะ
ต่อมาเราจะสร้างฟังก์ชัน NOT สำหรับกลับค่า true -> false และ false -> true ซึ่งกำหนดแบบนี้
NOT = λx . x FALSE TRUE
และเมื่อเดิม ขอเปลี่ยนชื่อเพื่อให้เข้าใจง่ายขึ้นอีกนิดนึง เป็น
NOT = λbool . bool FALSE TRUE
อธิบาย: ฟังก์ชัน NOT นั้นจะรับ boolean เข้าไป (อาจจะเป็น true หรือ false ก็ได้) แล้วเอาฟังก์ชันนั้น (อย่าลืมว่า true/false ในที่นี้ไม่ใช่ value แต่เป็น function) ไป apply หรือก็คือเอาไปรันกับค่า FALSE TRUE ที่วางเตรียมไว้
อาจจะยังไม่เห็นภาพ มายกตัวอย่างกัน
Case 1: NOT TRUE
NOT TRUE
-- แทนที่ NOT ด้วย Abstraction ที่เขียนไว้ข้างบน
(λbool . bool FALSE TRUE) TRUE
-- เอาค่า TRUE ใส่แทนพารามิเตอร์ bool ลงไป
-- จาก bool FALSE TRUE ก็จะได้เป็น
TRUE FALSE TRUE
-- เวลาอ่าน ให้อ่านจาก ซ้าย->ขวา
-- เราจะเจอ TRUE ก่อน, ก็ให้ไปดูว่าฟังก์ชัน TRUE มี Abstraction เป็นอะไร -> เอามาแทนที่ซะ
(λfirst . λsecond . first) FALSE TRUE
-- ฟังก์ชันนี้รับค่าเป็นพารามิเตอร์ 2 ตัว (คือ first, second) ก็ให้เอาค่า FALSE TRUE ใส่แทนที่ลงไป
-- ซึ่งฟังก์ชันของเราบอกว่ารับค่า first, second เข้าไป 2 ตัว
(λFALSE . λTRUE . FALSE)
-- แต่ให้ return first กลับไปตัวเดียว เลยได้ว่า
FALSE
ก็เลยสรุปได้ว่า NOT TRUE นั้นได้คำตอบเป็น FALSE นั่นเอง
** สำหรับคนที่เป็นโปรแกรมเมอร์สาย Imperative มา ถ้าอ่านอันนี้แล้วงง เราขอแปลงโค้ดทั้งหมดนี้ให้อยู่ในรูปของ Imperative ให้ดู
// สร้างตัวแปร TRUE, FALSE ให้เป็นฟังก์ชันที่รับ first, second ไปแล้วตอบกลับเป็น first, second ตามลำดับ
const TRUE = (first, second) => first
const FALSE = (first, second) => second
// จากนั้นสร้างฟังก์ชัน NOT ที่รับ bool ไป, แล้วเอาไปรันโดยส่งพารามิเตอร์เป็น FALSE, TRUE ลงไป
function NOT(bool){
return bool(FALSE, TRUE)
}
// ดังนั้น ถ้าเราต้องการหาค่า NOT TRUE เราก็ต้องสั่งว่า
NOT(TRUE)
// ซึ่ง TRUE จะถูกเอาไปแทนที่ตัวแปร bool
return bool(FALSE, TRUE)
// เลยจะกลายเป็น
return TRUE(FALSE, TRUE)
// ซึ่ง TRUE นั้นจริงๆ เป็นฟังก์ชันที่ return ค่าตัวแรกกลับไปเสมอ
// พารามิเตอร์ตัวแรกที่เราใส่ลงไปือค่า FALSE
// ดังนั้นสุดท้ายเราก็จะตอบกลับเป็นค่า FALSE
return FALSE
ซึ่งถ้าเราลองเอา NOT FALSE มาลองคิดด้วยหลักการเดียวกัน เราก็จะพบว่ามันออกมาเป็น TRUE ซึ่งถูกต้องแล้ว
Ex2: AND และ OR
มาดูตัวอย่างที่ 2 กันบ้าง ... คราวนี้เราลองมาคิดกับฟังก์ชันที่ซับซ้อนขึ้นกว่า NOT นั่นคือ AND กับ OR กันบ้าง
ทั้ง AND และ OR นั้นรับ boolean เข้าไป 2 ตัวแล้วให้ค่า boolean กลับมา
- โดย
ANDนั้นจะ returntrueถ้า input ทั้งสองค่าเป็นtrue, นอกนั้นจะตอบfalse - ส่วน
ORจะ returntrueถ้า input แม้แต่ตัวเดียวเป็นtrue, ซึ่งถ้าเป็นfalseทั้งคู่ถึงจะตอบfalse
แล้วถ้าเราจะเอามาเขียนแบบ Lambda Calculus เราจะทำยังไง?
AND
คำตอบที่ได้คือแบบนี้
AND = λx . λy . x y FALSE
อธิบาย: หากเราเอาค่า x และ y มา AND กัน เราจะได้ 2 เคสแบบนี้
- x มีค่าเป็น
true--> ก็ยังตอบไม่ได้ ต้องไปดูว่าค่า y เป็นtrueหรือfalse(แปลว่าถ้า x เป็นtrueคำตอบจะขึ้นอยู่กับตัวแปร y) - แต่ถ้า x เป็น
false--> ก็จบเลยไง! ไม่ต้องคิดตอบแล้ว
-- เริ่มด้วยการหาค่า x AND y
AND x y
-- ลองแทน x ด้วย TRUE (y ช่างมันก่อน ทิ้งมันเป็นตัวแปรไว้ตรงนั้นแหละ)
AND TRUE y
-- เอาฟังก์ชัน AND ที่ประกาศไว้ข้างบนมาแทนลงไป
(λx . λy . x y FALSE) TRUE y
-- แทนส่วนของ x ด้วย TRUE (y ก็คามันไว้เหมือนเดิมนะ)
TRUE y FALSE
-- ฟังก์ชัน TRUE บอกว่าให้ return first ดันนั้นให้ return y
y
อ่ะ ครึ่งแรกเสร็จและ ได้แบบนี้ ... ทีนี้ลองมาวิเคราะห์ตัว y ดูบ้าง ก็จะได้แบบนี้
-- ถ้า y เป็น TRUE
AND TRUE TRUE
-- ก็จะจบด้วยค่า TRUE (ค่าตัวที่สองหรือ second นั่นเอง)
TRUE
-- ถ้า y เป็น FALSE
AND TRUE FALSE
-- ก็จะจบด้วยค่า FALSE (ก็เป็นค่าตัวที่สองเหมือนเดิมนั่นแหละ แค่ครั้งนี้ค่ามันเป็น FALSE)
FALSE
ยังทันกันอยู่มั้ย?
มาลองดูเคสที่ x เป็น false กันบ้าง
-- ครั้งนี้, ลองแทน x ด้วย FALSE (y ช่างมันก่อนเหมือนเดิมนะ)
AND FALSE y
-- เอาฟังก์ชัน AND ที่ประกาศไว้ข้างบนมาแทนลงไป
(λx . λy . x y FALSE) FALSE y
-- แทนส่วนของ x ด้วย FALSE
FALSE y FALSE
-- ฟังก์ชัน FALSE บอกว่าให้ return second ดันนั้นให้ return FALSE (กลายเป็น y ไม่สนใจเลยนะ! ข้ามไปเลย)
FALSE
ดังนั้นแปลว่าถ้า x เป็น false ก็คือไม่ต้องดู y แล้ว ยังไงคำตอบก็ได้ FALSE ... โอ้ว ถูกต้องตามหลักการของ AND ในการเขียนโปรแกรมเลย!
OR
ยังไหวกันอยู่มั้ย (ฮา) มาต่อกันอีกตัวด้วย OR, ถ้าใครเริ่มเก็ต NOT กับ AND แล้วจะลองคิด OR เองก็ได้นะ ว่าจะสร้างฟังก์ชัน OR ยังไงดี?
เอาล่ะ มาดูคำตอบกัน
OR = λx . λy . x TRUE y
หลักการคล้ายๆ กันครับ คือเราต้องแบ่ง OR ออกเป็น 2 เคส
- x มีค่าเป็น
true--> อันนี้จะสลับกับ AND เพราะสามารถตอบได้เลยว่าtrue - แต่ถ้า x เป็น
false--> คราวนี้ต้องไปดูค่า y แทนแล้วว่า y เป็น boolean ตัวไหน
สำหรับทำไมถึงสร้างฟังก์ชันแบบนี้ขึ้นมา ถ้าคุณเก็ต AND แล้ว เมื่อเราเฉลยว่า OR มีโครงสร้างยังไง คุณน่าจะไล่เคสได้ไม่ยากเท่าไหร่ แต่ถ้ายังไล่เองไม่ได้ ลองกลับไปอ่านคำอธิบายเรื่อง AND ใหม่อีกรอบนะครับ
ทิ้งท้าย
จะตัวอย่าง จะเห็นว่า Lambda Calculus มีการประมวลผล term ต่างๆ ด้วยการกำหนดสัญลักษณ์ แล้วมีการยุบ/ขยายรวมเทอมต่างๆ ตามกฎที่ตั้งเอาไว้จนได้คำตอบออกมา ในหมดเป็นหลักการ ทำในกระดาษนี่แหละ แต่ก็แสดงหลักการว่าเราคำนวณค่าต่างๆ ได้อย่างไรออกมาได้ดีมาก
ปลายทางของทางสายนี้ มุ่งสู่ Functional Programming
มีคนบอกว่าภาษาโปรแกรมทุกภาษา หากไปวิเคราะห์แก่นของมันจริงๆ เราจะได้ Lambda Calculus ออกมา (คือเอาพวก syntax if-else หรือพวก for อะไรพวกนั้นออกไปน่ะนะ) ซึ่งถ้ายึดตามที่บอกไปข้างต้นว่า Lambda Calculus นั้นมันเทียบได้กับ Turing Machine จะบอกแบบนั้นมันก็ถูกแหละ (ฮา)
แต่แนวคิดก็จะไม่เหมือนกัน คือถ้าเรายึดหลักการของ Turing Machine ซึ่งเป็น State-Base การเรียนรู้ก็จะเข้าใจได้ง่าย ตรงไปตรงมา เน้นการแปลงโจทย์ให้กลายเป็นลำดับ Algorithm ที่ส่วนใหญ่ก็จะเป็นการเซ็ตค่าไปๆ มาๆ บนหน่วยความจำ (สังเกตว่าส่วนใหญ่ Algorithm จะพูดถึงแต่การกำหนดและเซ็ตค่าตัวแปรเป็นหลักเลย)
แต่เนื่องจากคอมพิวเตอร์ไม่มีเซ้นซ์ความคิดอะไรเลย ถ้าเราเรียงลำดับ Algorithm ผิดไปแม้แต่นิดเดียว หรืออาจจะลืมกำหนดอะไรบางเคส แน่นอนว่าโปรแกรมก็จะทำงานผิดไปเลย (ที่เราเรียกว่า "บั๊ก" ยังไงล่ะ!) ตัวอย่างคลาสสิกๆ ที่ทุกคนน่าจะเคยเจอ เช่นเขียน loop แล้วกำหนดค่าเริ่มตัวผิด หรือลืมใส่ update i++ อะไรแบบนั้น, หรือถ้าทำงานกับ int ก็อาจจะลืมกรณีที่ int สามารถติดลบได้ บลาๆๆ
ถ้าเราเขียนโปรแกรมด้วย Functional Programming แล้วโอกาสที่เราจะลืมอะไรพวกนั้นจะน้อยลงมากๆ (บางคนก็บอกเลยว่าเขียน Functional Programming แล้วจะ Bug-Free! เลยนะ ... ซึ่งเราคิดว่าไม่ยังไม่ถึงขนาดนั้น มันแค่จะทำให้โปรแกรมบั๊กน้อยลงมากๆๆ แต่ยังไม่ถึงกับไม่มีบั๊กเลยนะ) เพราะในการเขียนเราจะได้โฟกัสไปยังหลักวิธีแก้ปัญหาแท้ๆ โดยไม่ต้องไปกังวลกับการจัดการเมมโมรี่หรือเรื่องยิบย่อยอื่นๆ เลย
สำหรับ Lambda Calculus นั้นยังมีเนื้อหาให้ศึกษาต่ออีกมากมาย เช่นถ้าเราจะเขียน loop เราจะต้องทำยังไงล่ะ (สปอยล์: Functional Programming ไม่มี loop ล่ะ!!) ถ้าใครสนใจก็ลองศึกษาต่อเอานะ ... แต่ในบล็อกนี้ก็คงจบหัวข้อนี้แค่นี้แหละ ต่อไปเราจะไปโฟกัสกับเรื่องของ Functional Programming กันแทน (คนเขียนเป็นเด็กcom ไม่ใช่เด็กmathนะ ฮา)








1 Response
[…] อ่านเพิ่มเติมได้ที่ บทความ Lambda Calculus และบทความ Category […]